Почему умножение матриц быстрее в numpy, чем в ctypes в Python?
Я пытался найти самый быстрый способ умножения матриц и пробовал 3 разных способа:
Pure python implementation: no surprises here. Numpy implementation usingnumpy.dot(a, b)
Interfacing with C using ctypes module in Python.
Это код C, который преобразуется в общую библиотеку:
<code>#include <stdio.h>
#include <stdlib.h>
void matmult(float* a, float* b, float* c, int n) {
int i = 0;
int j = 0;
int k = 0;
/*float* c = malloc(nay * sizeof(float));*/
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
int sub = 0;
for (k = 0; k < n; k++) {
sub = sub + a[i * n + k] * b[k * n + j];
}
c[i * n + j] = sub;
}
}
return ;
}
</code>
И код Python, который вызывает его:
<code>def C_mat_mult(a, b):
libmatmult = ctypes.CDLL("./matmult.so")
dima = len(a) * len(a)
dimb = len(b) * len(b)
array_a = ctypes.c_float * dima
array_b = ctypes.c_float * dimb
array_c = ctypes.c_float * dima
suma = array_a()
sumb = array_b()
sumc = array_c()
inda = 0
for i in range(0, len(a)):
for j in range(0, len(a[i])):
suma[inda] = a[i][j]
inda = inda + 1
indb = 0
for i in range(0, len(b)):
for j in range(0, len(b[i])):
sumb[indb] = b[i][j]
indb = indb + 1
libmatmult.matmult(ctypes.byref(suma), ctypes.byref(sumb), ctypes.byref(sumc), 2);
res = numpy.zeros([len(a), len(a)])
indc = 0
for i in range(0, len(sumc)):
res[indc][i % len(a)] = sumc[i]
if i % len(a) == len(a) - 1:
indc = indc + 1
return res
</code>
Я бы поспорил, что версия, использующая C, была бы быстрее ... и я проиграл! Ниже мой тест, который, кажется, показывает, что я сделал это неправильно, или чтоnumpy тупо быстро
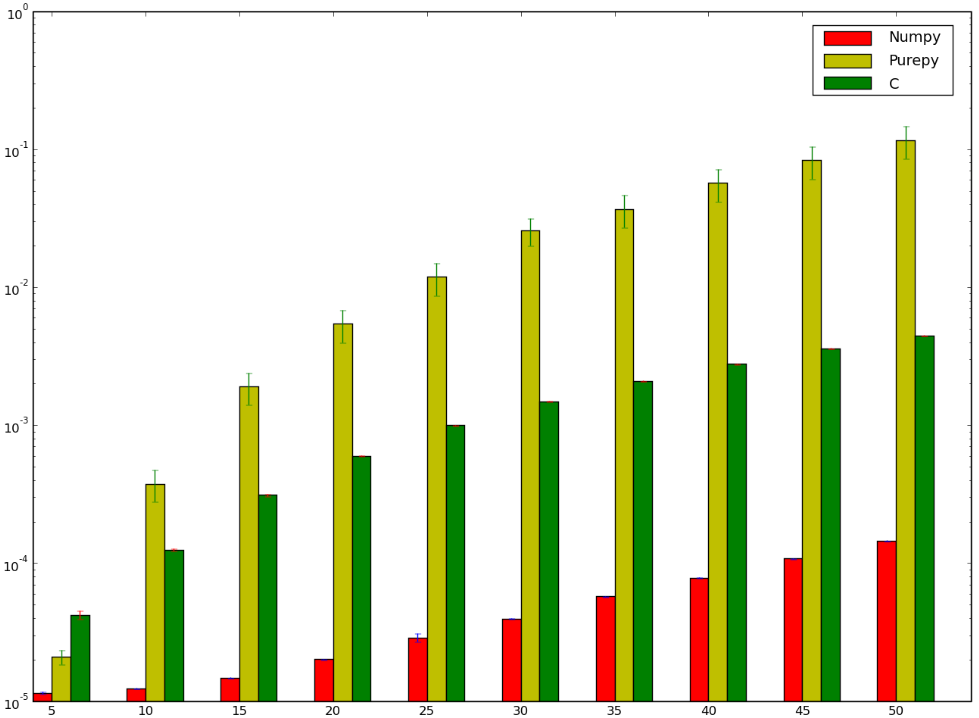
Я хотел бы понять, почемуnumpy версия быстрее, чемctypes версия, я даже не говорю о чистой реализации Python, так как это отчасти очевидно.