Я пытаюсь повторить сюжет в «Орбитальной механике» Кертиса, но я просто могуне совсем понял. Тем не менее, я сделал главный путь, переключившись наnp.arctan2 от .np.arctan

Может быть, я реализуюarctan2 неправильно?

import pylab
import numpy as np

e = np.arange(0.0, 1.0, 0.15).reshape(-1, 1)

nu = np.linspace(0.001, 2 * np.pi - 0.001, 50000)
M2evals = (2 * np.arctan2(1, 1 / (((1 - e) / (1 + e)) ** 0.5 * np.tan(nu / 2) -
           e * (1 - e ** 2) ** 0.5 * np.sin(nu) / (1 + e * np.cos(nu)))))

fig2 = pylab.figure()
ax2 = fig2.add_subplot(111)

for Me2, _e in zip(M2evals, e.ravel()):
    ax2.plot(nu.ravel(), Me2, label = str(_e))

pylab.legend()
pylab.xlim((0, 7.75))
pylab.ylim((0, 2 * np.pi))
pylab.show()

На изображении ниже появляются разрывы. Предполагается, что функция должна быть плавной и соединяться при 0 и 2 пи в диапазоне y (0, 2pi), не касаясь 0 и 2pi.

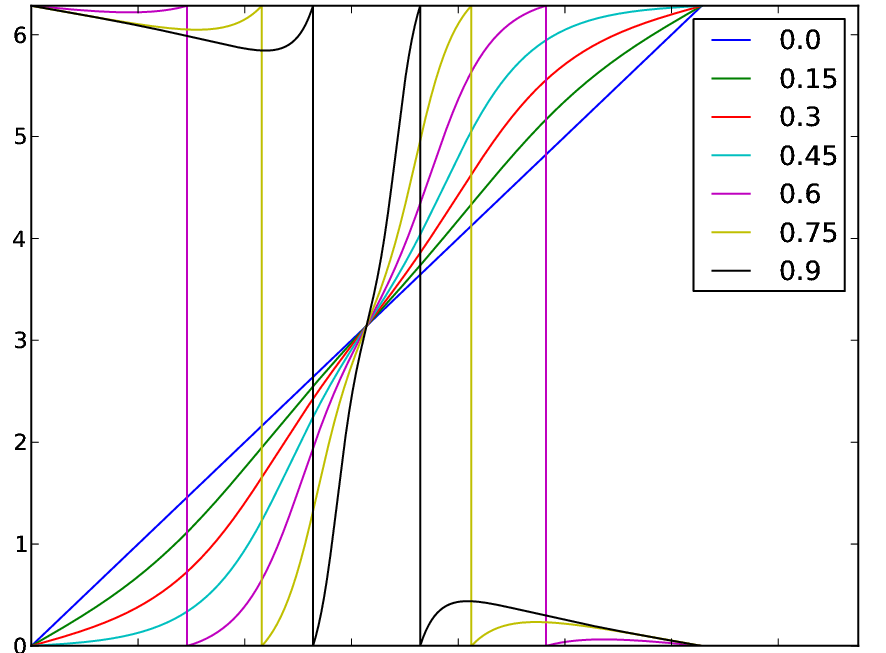
Учебник сюжет и уравнение:

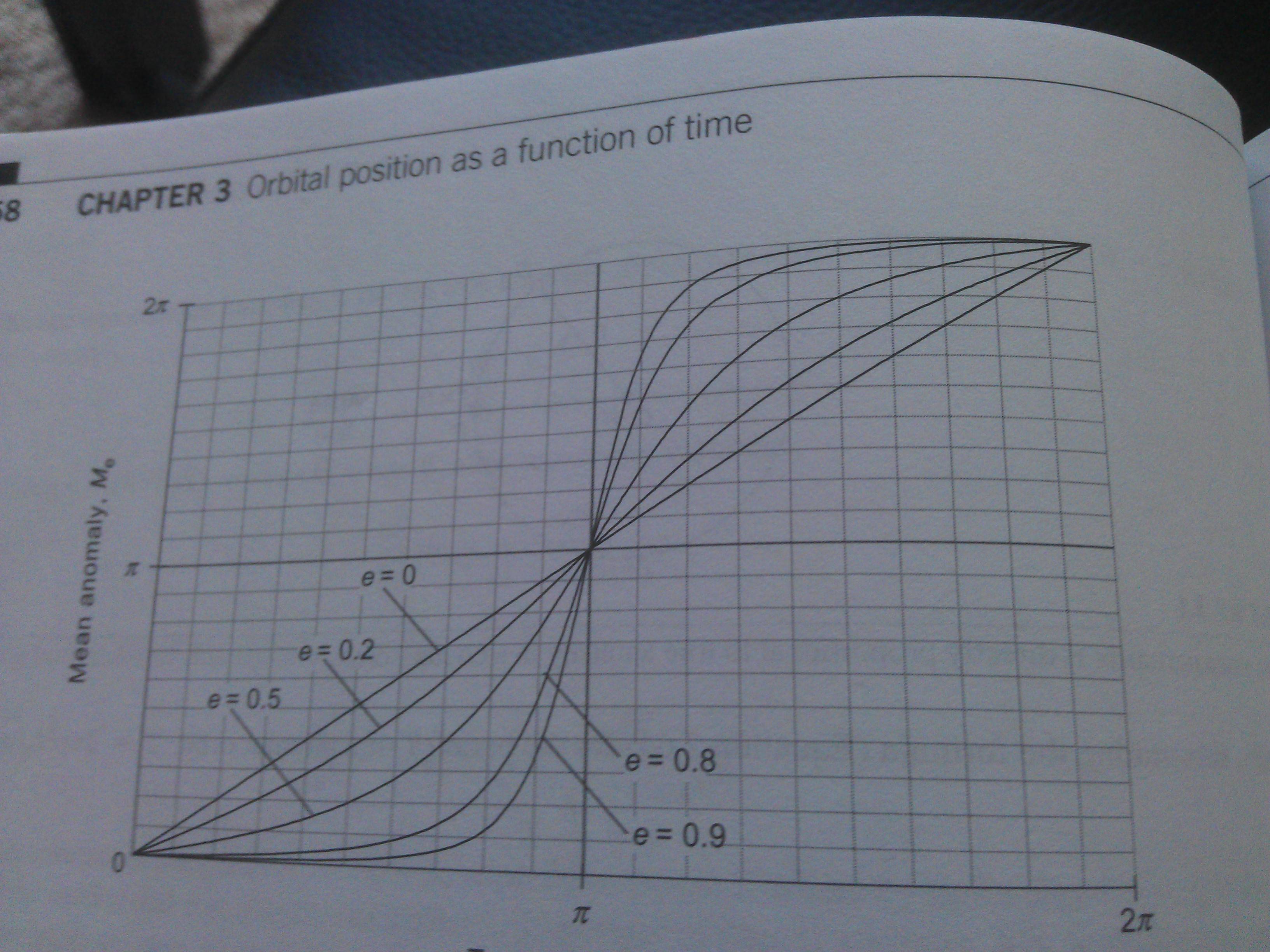
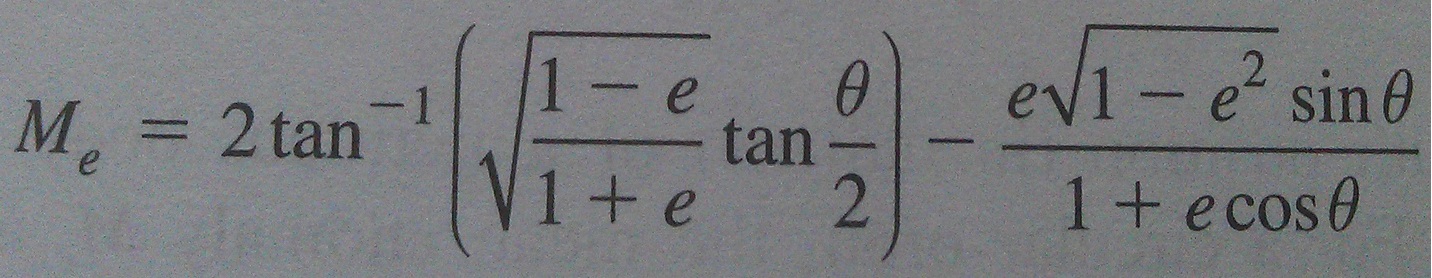
По просьбе Сулло Кастро мне сказали, что:

Проблема может заключаться в функции арктана, которая дает "Основные ценности » в качестве вывода.

Таким образом, arctan (tan (x)) не дает x, если x является углом во втором или третьем квадранте. Если вы построите график arctan (tan (x)) от x = 0 до x = Pi, вы обнаружите, что он имеет скачкообразный скачок при x = Pi / 2.

В вашем случае вместо написания arctan (arg), я полагаю, вы бы написали arctan2 (1, 1 / arg), где arg - аргумент вашей функции arctan. Таким образом, когда arg становится отрицательным, arctan2 даст угол во втором квадранте, а не в четвертом. "