Эти полосы спектра раньше судили по глазу, как это сделать программно?
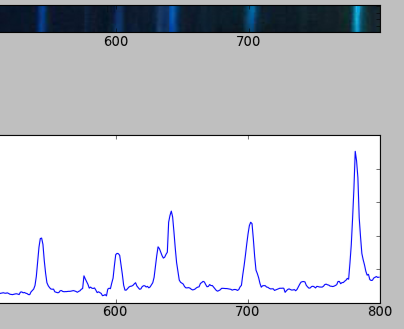
Операторы использовали для изучения спектра, зная местоположение иwidth каждой вершины и оцените часть, к которой принадлежит спектр. По-новому, изображение захватывается камерой на экран. И ширина каждой полосы должна быть рассчитана программно.
Старая система: спектроскоп - & gt; человеческий глаз Новая система: спектроскоп - & gt; камера - & gt; программа
Что является хорошим методом дляcompute the width of each band, учитывая их приблизительное положение по оси X; учитывая, что эта задача раньше выполнялась на глаз, а теперь должна выполняться программой?
Извините, если мне не хватает деталей, но их мало.
Список программ, сгенерировавших предыдущий график; Надеюсь это актуально
import Image
from scipy import *
from scipy.optimize import leastsq
# Load the picture with PIL, process if needed
pic = asarray(Image.open("spectrum.jpg"))
# Average the pixel values along vertical axis
pic_avg = pic.mean(axis=2)
projection = pic_avg.sum(axis=0)
# Set the min value to zero for a nice fit
projection /= projection.mean()
projection -= projection.min()
#print projection
# Fit function, two gaussians, adjust as needed
def fitfunc(p,x):
return p[0]*exp(-(x-p[1])**2/(2.0*p[2]**2)) + \
p[3]*exp(-(x-p[4])**2/(2.0*p[5]**2))
errfunc = lambda p, x, y: fitfunc(p,x)-y
# Use scipy to fit, p0 is inital guess
p0 = array([0,20,1,0,75,10])
X = xrange(len(projection))
p1, success = leastsq(errfunc, p0, args=(X,projection))
Y = fitfunc(p1,X)
# Output the result
print "Mean values at: ", p1[1], p1[4]
# Plot the result
from pylab import *
#subplot(211)
#imshow(pic)
#subplot(223)
#plot(projection)
#subplot(224)
#plot(X,Y,'r',lw=5)
#show()
subplot(311)
imshow(pic)
subplot(312)
plot(projection)
subplot(313)
plot(X,Y,'r',lw=5)
show()